今天我們來看看我覺得超可愛的資料結構Tree，中文叫做樹，Tree跟LinkedList有一點像，更精確地說，LinkedList是一種特別的Tree，先不要講太多，我們直接開始介紹Tree。

Tree也是利用節點(Node)的形式來存取資料，結點有包含資料跟指向下一層Node的指標，跟LinkList比較不同的是，指向下一層的指標不會只指向一個Node，而是會指向多個Node。
我們先來看看樹長怎麼樣吧！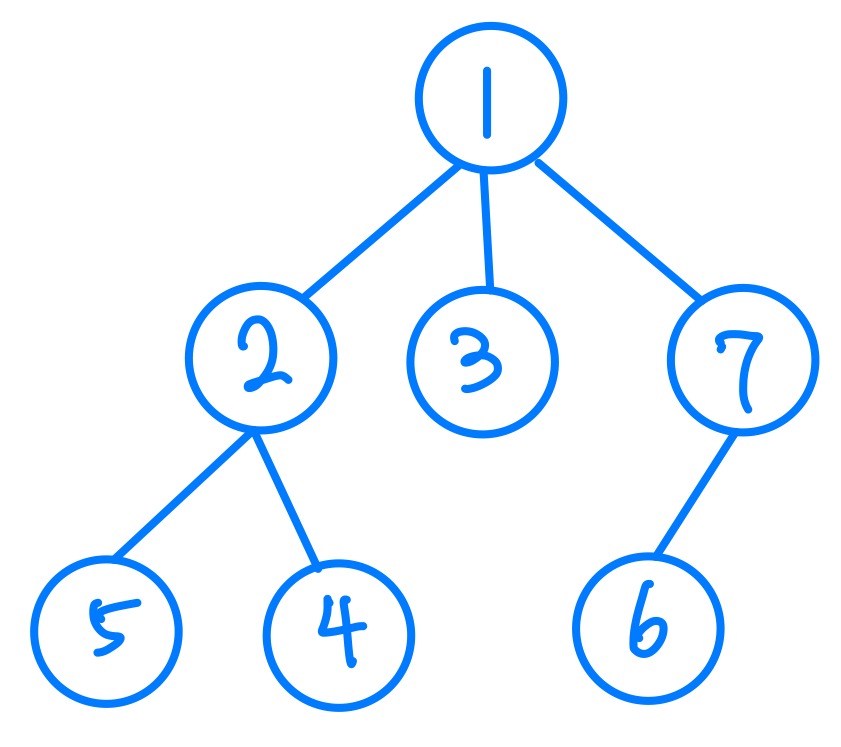

關於Tree的一些術語

Tree有他一些專業的術語，在這邊跟大家說比較常見的幾個詞。

• Root Node(根節點): 最上層的Node，沒有任何Node指向他。
• Leaf Node(樹葉節點): 最底層的Node，他們沒有指向任何人，也就像樹葉一樣長在樹的最外面。
• Tree Depth(樹的深度): 從Root Node到最深的Leaf Node的高度，也可以稱作樹的高度。
• Parent Node(父節點) : 一個Node的Parent Node就是指上層連接它的Node，除了Root Node以外，其他Node會有Parent Node。以圖上的例子1就是2、3、7的父節點，2就是5、4的父節點等等。
• Child Node(子節點) : 一個Node的Child Node 就是指他下層所連接的Node，除了Leaf Node以外，其他Node都會有Child Node。以圖上的例子1的子節點就是2、3、7，7的子節點就是6等等。
  

二元樹 BinaryTree(BT)!

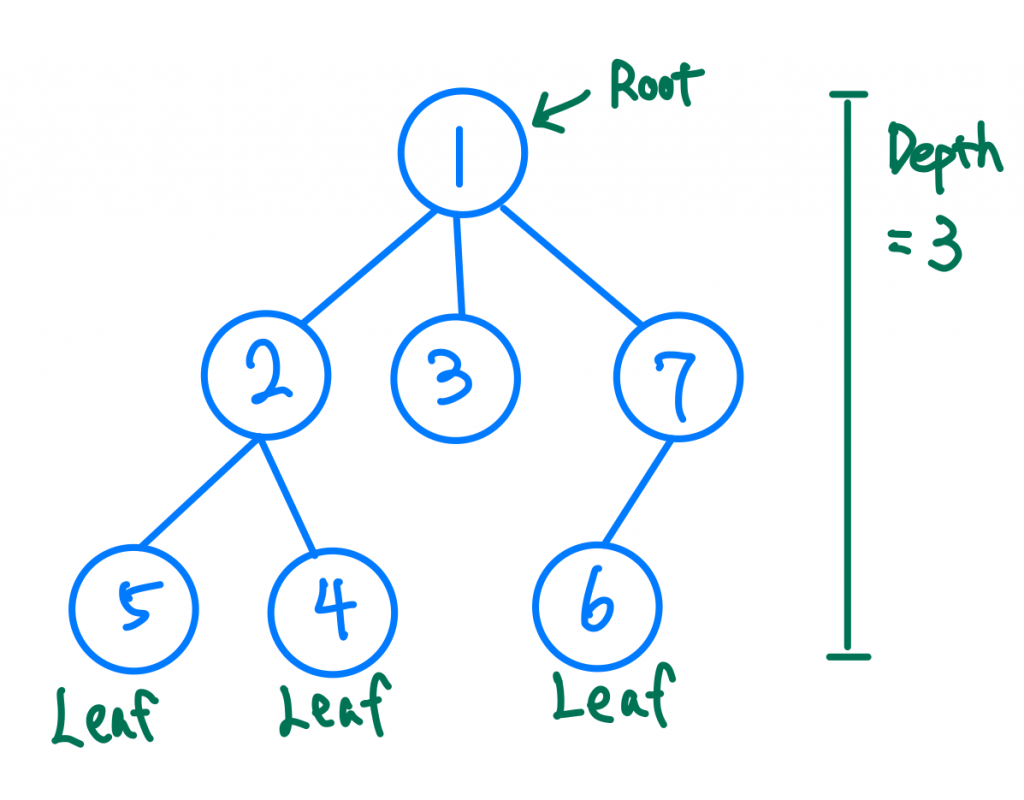
前面我們說到Tree裏頭一個Node可以有多個Child Node，那如果我們限制他只能有兩個Child Node的話，那他就是Binary Tree了，中文我們叫二元樹。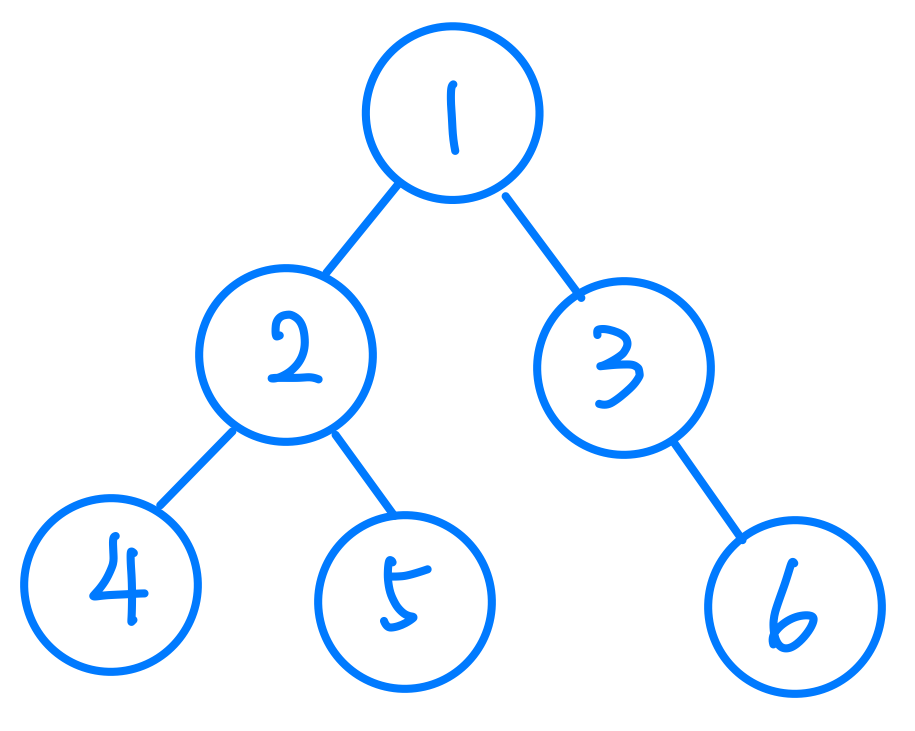

二元搜尋樹 Binary Search Tree (BST)

Binary Search Tree是一種特別的Binary Tree，雖然說特別，但在Tree裡面，Binary Search Tree是更常用的一種資料結構，那為什麼他那麼紅呢？我們先來看看他的特性。

Binary Search Tree是一種特別的Binary Tree所以他也是一個Node只有兩個Child，但是特別的是，左子節點的值始終小於我現在這個節點的值，右子節點的值始終大於我現在這個節點的值，對於我其他的子節點也是這樣的定義。說起來有點亂，但是我們來看一下圖就會發現清楚很多。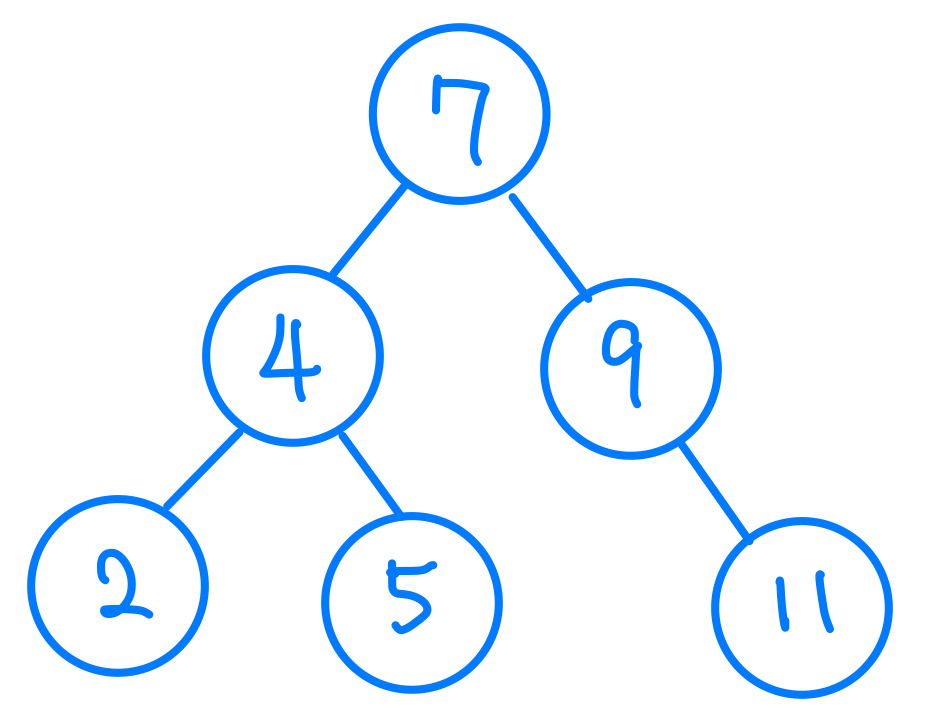

圖中我們會發現對每一個node而言，我的左邊的node值都會比我小，右邊的node值都會比我大。
大家先記得它的特性，後面的篇幅我們就會知道為什麼BST那麼厲害囉。

完美二元樹的特性

假設我們的樹節點都是滿的，這種樹我們稱作完美二元樹。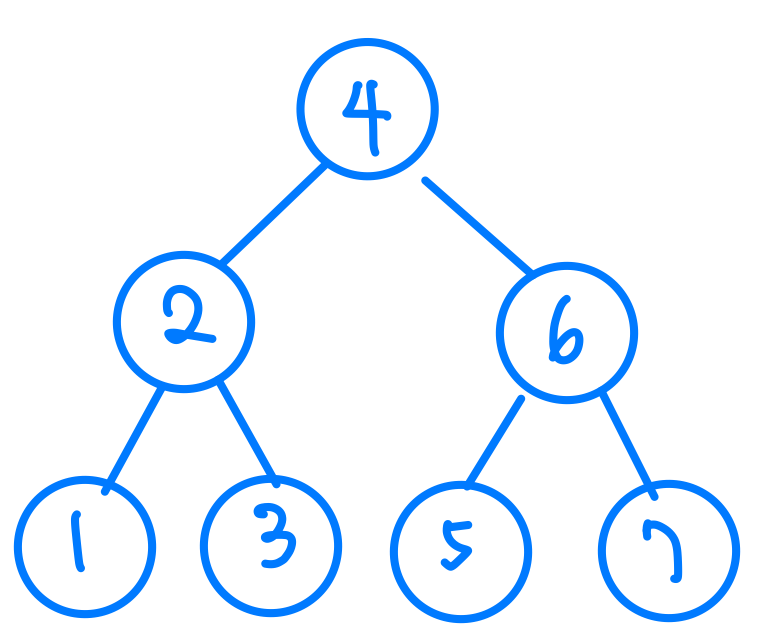

因為我們的節點都是1個生出2個的關係，第0層(也就是最上面只有一個根節點的那層)。會生出2個節點給第1層，第1層的2個節點也會分別生出兩個節點給第2層，所以第2層會有4個節點，以此類推我們可以知道任何一層的節點數會是上一層的2倍，假如一個完美的3層BST，他會有2^0+2^1+2^2個節點數，也就是7個節點。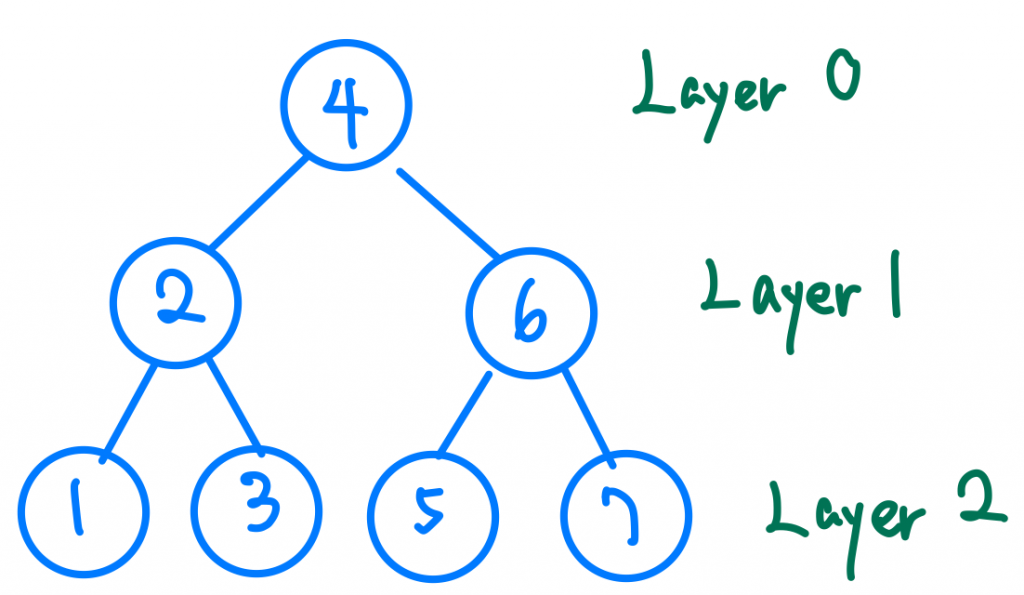

二的次方其實有一點有趣，大家可以嘗試去計算會發現2^n會等於 1+2^0+2^1+⋯+2^(n-1)
舉個簡單的例子 2^3=8, 2^0=1, 2^1=2, 2^2=4, 8=1+1+2+4。

也因為這樣的特性我們可以說在完美的BST(BT)裏，最下面一層的節點數會等於從頭一直加到他上一層的節點數+1。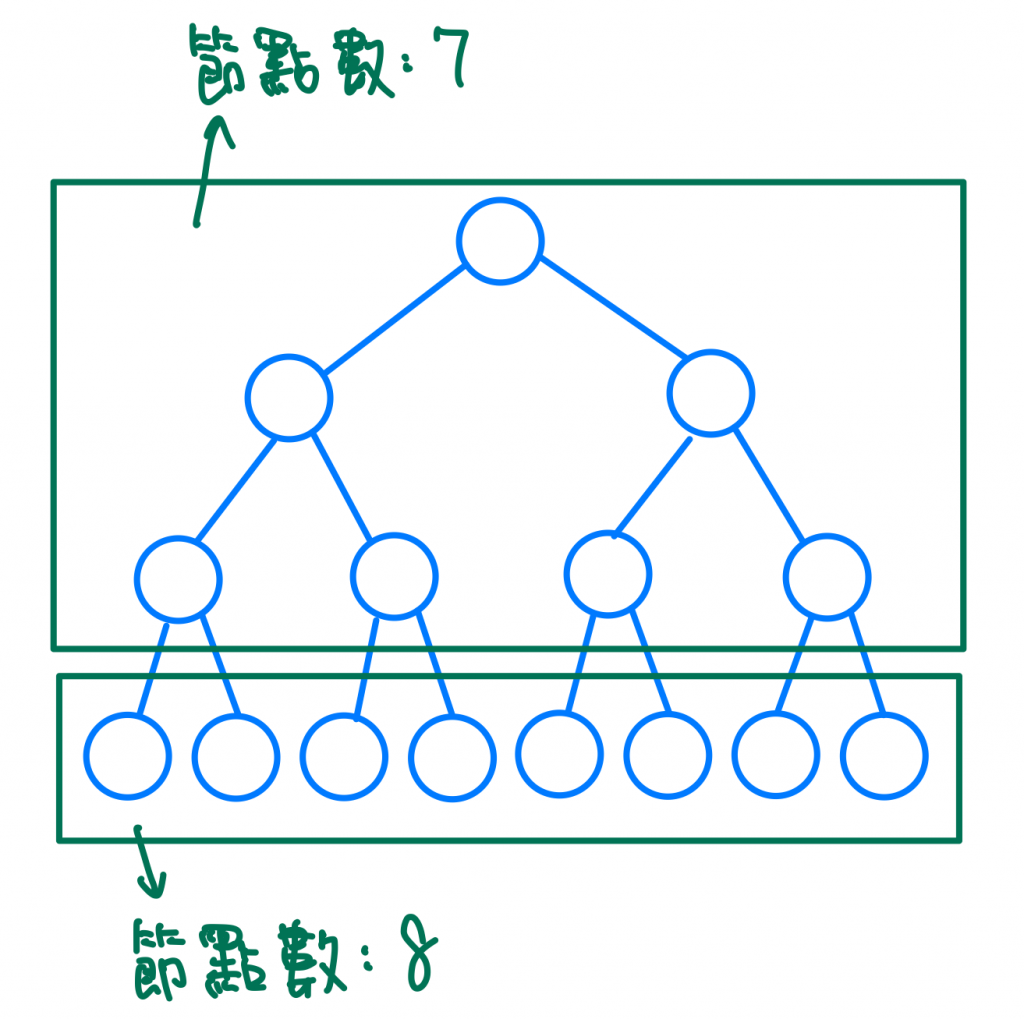

把以上的事情歸納一下我們可以發現，2層的完美二元樹會有2^2-1個節點，3層的完美二元樹會有2^3-1個節點，為了方便計算，我們不用太在意那個減一(記得嗎在時間複雜度裡，常數項我們是可以直接忽略它的)，由此可知我們可以說n層的完美二元樹會有2^n個節點。
我們現在反過來想，假如有8個節點(實際上是7個)的BT我們要怎麼知道他有幾層呢？

我們現在令層為layer、節點樹為n，上面例子我們可以知道，2^layer=8大家可以翻一下高中的數學課本後會發現，layer就可以用我們所謂的log來表示，layer=log以2為底n 。記得在時間複雜裡，我們其實不那麼重視常數項，所以可以間接表示成layer=log n，換句話說數的高度就是log n，n是樹的節點數量。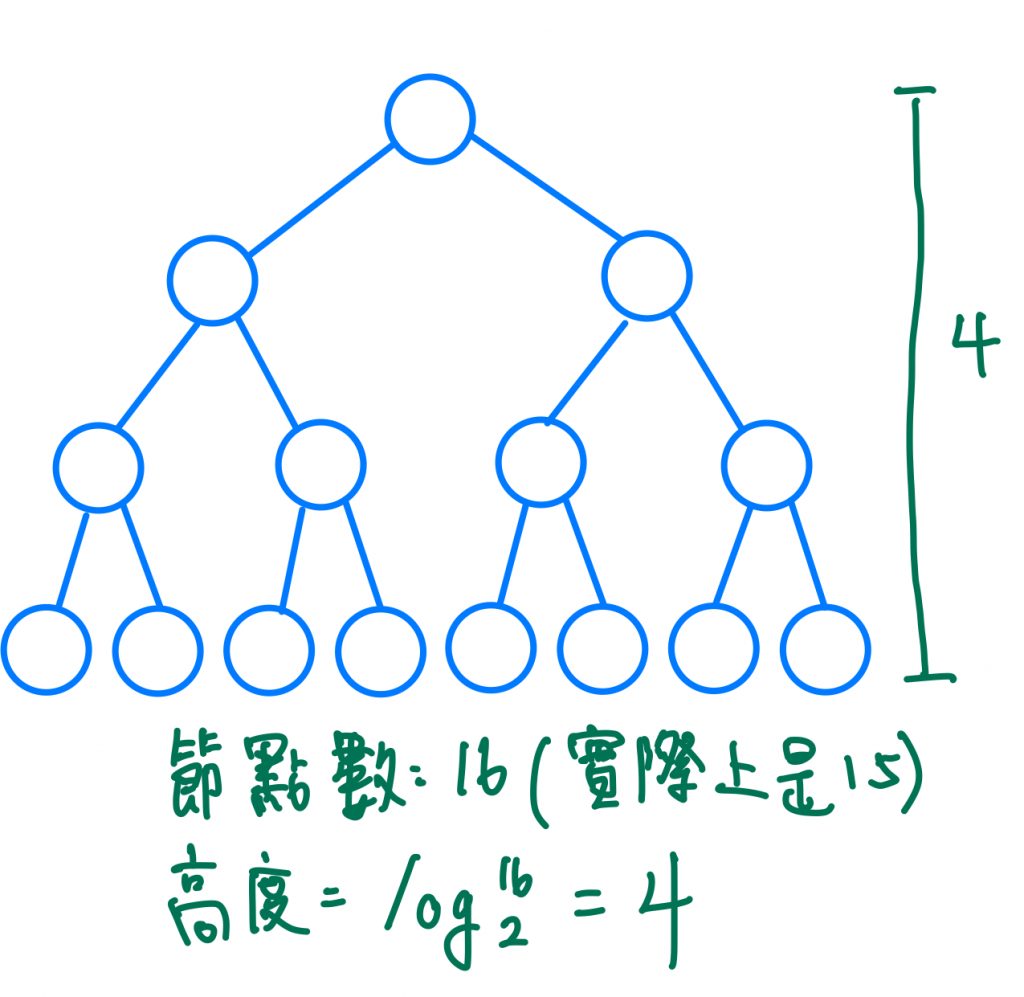

好的樹的章節目前先講到這邊，大家一定要記得log n的概念，因為明天我們將要先進入一個資訊人必須知道的演算法。

結論

樹是一種相當重要的資料結構，如果有讀者之前是遇到Log n這種時間複雜度卻不太了解的，我建議可以從樹開始想起，會明白的許多喔！
當然樹還有一些平衡樹、完全二元樹這些定義，大家有興趣可以去上網查看看，其實並不會很複雜，我在這邊就不概述了。
對了，因為我不曉得的怎麼使用這個平台的數學公式打出那種log以2為底還有2^(n-1)這種表示法，所以我先以目前大家看到的方式呈現，如果有讀者願意告訴我也很歡迎私訊我，我會很感謝您的。